Divers témoignages sur des excès de fausses-couches et de décès de nourrissons dans différents pays peuvent actuellement nous interroger. L’objet de cet article est l’étude de la mortalité néonatale, c’est-à-dire la mortalité des nourrissons de la naissance à l’âge de 28 jours révolus. Les mortalités néonatales de trois pays, Ecosse, France et Israël seront évoquées.
1) Analyse et méthodologie
Les analyses suivantes sont réalisées à partir de données officielles.
Les études portent sur l’évolution des taux mensuels de mortalités des nourrissons à partir de 2018.
Ces taux sont calculés pour chaque mois par le ratio du nombre de bébés décédés natifs du mois étudié sur le nombre de naissances du mois.
Les taux sont comparés à un taux de référence, calculé de janvier 2018 à décembre 2019. L’année 2020 a été exclue du calcul du taux de référence. En effet, une sous-mortalité a été observée chez les enfants nés en 2020. Cette sous-mortalité est sans doute due aux contraintes sanitaires imposées, comme les confinements, les couvre-feux, etc... (Figures 4 et 5 des annexes respectives A et B).
Les comparaisons statistiques sont effectuées avec la loi de Poisson (annexe H pour plus de détails).
Pour chaque mois, le taux de décès attendus est calculé à l'aide du taux de référence.
Sur les graphiques, l’intervalle de confiance des taux à 95 % est indiqué en pointillés bleus. Le taux de mortalité a une probabilité de 95 % de se trouver dans l’intervalle et de 5 % de se trouver hors de l’intervalle. L’intervalle de confiance à 99,8 % est indiqué en pointillés rouges. Le taux de mortalité a une probabilité de 99,8 % de se trouver dans l’intervalle et de 2 ‰ de se retrouver hors de l’intervalle.
Il est ainsi possible de repérer les taux anormaux qui dépassent des intervalles de confiance à 99,8 %.
2) Données françaises
Les nombres de naissances [1] et de décès [2] sont issues des données officielle de l'INSEE.
Le graphique des taux mensuels de mortalité néonatale, décès de la naissance à 28 jours, de janvier 2018 à septembre 2022 est représenté à la figure 1.
Les intervalles de confiance ont été calculés avec la loi de Poisson.

Taux de référence (janvier 2018-décembre 2019) = 2,69 décès / 1 000 naissances
lien : http://caillou5310.free.fr/index_alertez_bb.php#mort_inf_0_29
Le taux de mortalité de référence 2018-2019 est de 2,69 décès pour 1 000 naissances (ligne verte).
La ligne rouge pointillée verticale indique le mois de mai 2021, mois où les personnes majeures ont été éligibles aux vaccinations anti covid19. Il est à noter que, dès le mois d'avril 2021, les femmes enceintes à partir du second mois de grossesse étaient prioritaires pour la vaccination.
Nous observons les taux de mortalité dans la norme sauf pour les bébés nés en juin 2021, où le taux de mortalité néonatale est de 3,48 décès pour 1 000 naissances. Ce taux, hors de l’intervalle de confiance à 99,8 % est hautement significatif à 0,16 ‰ : soient 212 décès à moins de 28 jours pour 60 857 naissances vivantes, alors qu’environ 164 étaient attendus (intervalle de confiance à 99,8 % compris entre 125 et 203).
La mortalité néonatale (décès entre la naissance et 28 jours révolus) se décompose en
- mortalité néonatale précoce: décès entre la naissance et 6 jours révolus
- mortalité néonatale tardive: décès entre 7 jours et 28 jours révolus
Selon la même méthodologie, les graphiques représentant les taux de mortalité néonatale précoce (taux de référence = 1,83 / 1 000) et tardive (taux de référence = 0,85 / 1 000) sont présentés respectivement dans les figure 6 (annexe C) et 7 (annexe D).
Nous observons, pour la mortalité néonatale précoce, un pic hautement significatif pour les bébés nés en juin 2021 à 2,58 décès pour 1 000 naissances vivantes. Ce pic en dehors de l'intervalle de confiance à 99,8 % est hautement significatif à 0,029 ‰ : soient 157 décès alors qu'environ 112 sont attendus (intervalle de confiance à 99,8 % compris entre 80 et 145).
Aucun pic hautement significatif n'est constaté pour les mortalités néonatales tardives.
Nous pouvons en déduire que la mortalité néonatale excessive observée pour les bébés nés en juin 2021 est la conséquence de la mortalité néonatale précoce.
La mortalité néonatale précoce} a été décomposée en deux modalités :
- mortalité à moins de 48h de vie
- mortalité entre 2 jours et 6 jours révolus de vie
Selon la même méthodologie, les graphiques représentant les taux de mortalité à moins de 48h (taux de référence = 1,15 / 1 000) et tardive (taux de référence = 0,69 / 1 000) sont présentés respectivement dans les figures 8 (annexe E) et 9 (annexe F).
Nous observons, pour la mortalité à moins de 48h, un pic hautement significatif pour les bébés nés en juin 2021 à 1,69 décès pour 1 000 naissances vivantes. Ce pic en dehors de l'intervalle de confiance à 99,8 % est significatif à 0,12 ‰ : soient 103 décès alors qu'environ 70 sont attendus (intervalle de confiance à 99,8 % compris entre 45 et 96).
Aucun pic hautement significatif n'est constaté pour les mortalités entre 2 et 6 jours révolus. Nous observons néanmoins un pic en juin 2021, à la limite de la significativité à 95 %.
Ce pic de juin 2021 se retrouve bien entendu dans le graphique de mortalité infantile (décès entre la naissance et un an) de la figure 4 de l'annexe A. Il est significatif à 0,733 ‰. Il est la résultante des décès néonataux en phase précoce. En effet, il n'y a aucun pic significatif, en 2021, dans le graphique de la mortalité post-néonatale (décès entre un mois et un an) de la figure 5 de l'annexe B.
Nous pouvons en déduire que la mortalité néonatale excessive observée pour les bébés nés en juin 2021 est majoritairement due à la mortalité des nourrissons à moins de 48h.
Que s'est-il passé en France pour avoir, un taux aussi élevé de mortalité néonatale précoce des bébés natifs de juin 2021 ?
3) Données écossaises
Les données écossaises pour réaliser cette étude sont les données officielles, disponibles sur le site de santé publique écossaise [3].
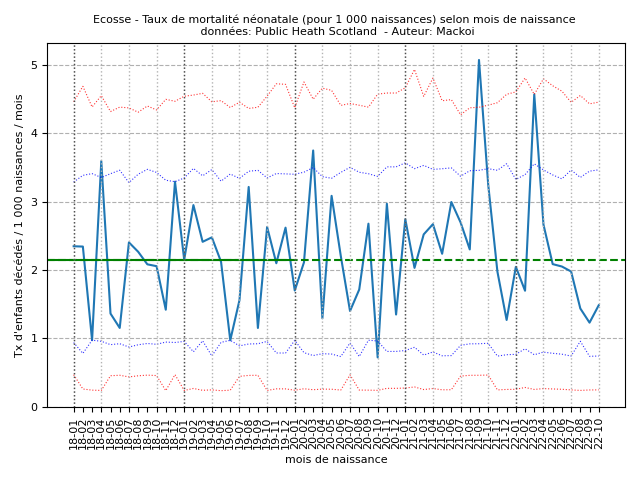
Les taux mensuels de mortalité néonatale (décès de la naissance à 28 jours révolus) de juillet 2017 à octobre 2022 sont représentés sur la figure 2.
Les différences par rapport à l'analyse de la mortalité néonatale française sont les suivantes :
- Le calcul du taux de référence va de juillet 2017 à décembre 2019.
- Les taux de mortalité néonatale sont calculés pour chaque mois par le ratio du nombre de bébés décédés dans le mois (mais pas nécessairement nés ce mois-ci) sur le nombre de bébés nés dans le mois.
- Les intervalles de confiance sont calculés par une loi Binomiale.
- Les intervalles de confiance sont à un peu plus de 95 % (soit deux écart-types, nommé "warning limits") et à un peu plus de 97 ‰ (soit trois écart-types, nommé "control limits").
- Les ordres de grandeur du nombre de naissances vivantes mensuelles sont différents: Ils sont autour de 4 000 en Écosse et 63 000 en France.
Le taux de référence est de 2,15 décès pour 1 000 naissances vivantes.
Nous observons de mars 2021 à octobre 2021, huit taux mensuels consécutifs supérieurs au taux de référence (points bleus). Deux taux mensuels de mortalité néonatale hautement significatifs hors de la limite de contrôle sont observés : un en septembre 2021 avec 5,1 décès pour 1 000 naissances et un en mars 2022 avec 4,6 décès pour 1 000 naissances. Ces deux taux font plus de deux fois le taux de référence.
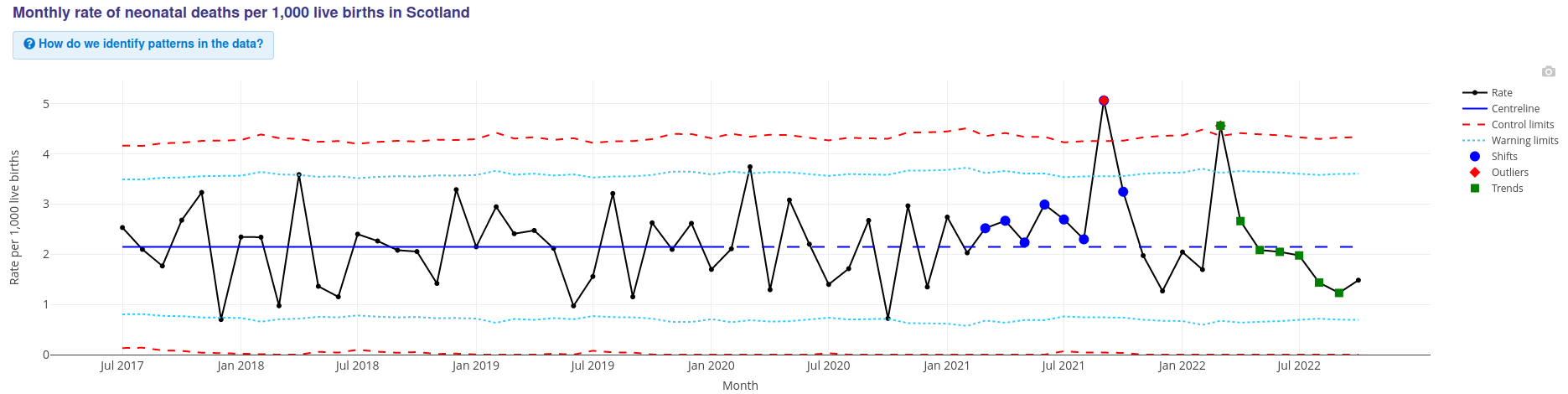
Taux de référence (janvier 2018-décembre 2019) = 2,14 décès / 1 000 naissances
lien : https://scotland.shinyapps.io/phs-covid-wider-impact/
Le jeu de données écossais étant disponible, un graphique a été réalisé avec la méthodologie utilisée sur les données françaises (figure 10 de l'annexe G).
Nous observons les deux mêmes pics de mortalité hautement significatifs en septembre 2021 (significatif à 0,27 ‰) et en mars 2022 (significatif à 2,82 ‰).
Que s’est-il passé en Ecosse pour qu’en moins d’un an, le taux mensuel de mortalité néonatale dépasse à deux reprises la limite supérieure de contrôle ?
Le docteur John Campbell s'est alarmé de ces deux pics de mortalité néonatale dans sa vidéo du 20 octobre 2022 :
https://www.youtube.com/watch?v=wj4rE0LrpR0Il nous indique qu'ils seraient les plus élevés depuis 10 ans.
4) Données israéliennes
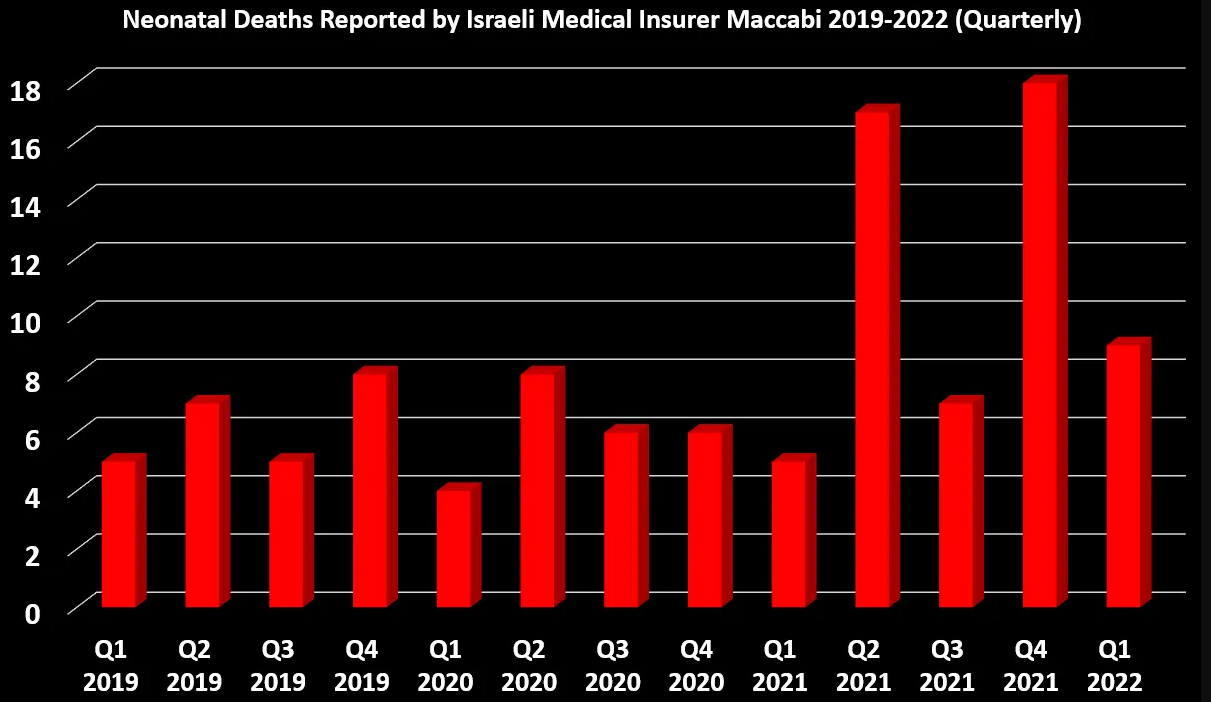
lien : https://jackanapes.substack.com/p/data-on-neonatal-deaths-from-major
Les nombres de décès des bébés à moins de 28 jours, par trimestre, sont représentés dans la figure 3.
Ces données ont été obtenues par une requête FOIA de l'économiste David Shuldman au gouvernement israélien et sont rapportées dans un article du docteur Josh Guetzkow [4]. Ce sont les données de l'assurance maladie israélienne Maccabi, qui couvre environ 25 % des israéliens.
Nous pouvons nettement voir deux pics, au second et quatrième trimestre 2021 avec plus de 17 décès, alors qu'habituellement, il y en a entre 5 et 8. S'il n'est pas possible de calculer les taux de mortalité avec exactitude et de faire une analyse statistique, nous savons néanmoins que les nombres de naissances trimestriels restent du même ordre de grandeur (compris entre 10 500 et 12 200). Il est donc évident que ces deux pics de mortalité néonataux, laissent peu de doute quant à leur significativité.
Il est à noter qu'il y a eu des campagnes vaccinales pour les femmes enceintes à partir du second trimestre de grossesse un à trois mois avant chaque pic.
Que s’est-il passé en Israël pour que la mortalité néonatale prenne de telles proportions à partir du second trimestre 2021 ?
5) Éléments de réflexion
Pour la France, le pic d'excès de mortalité néonatale en juin 2021 correspond à la mortalité néonatale précoce et plus particulièrement à moins de 2 jours de vie. Ces informations ne sont pas disponibles pour l'Écosse et Israël.
La mortalité périnatale englobe la mortinatalité (mort in utéro) et la mortalité néonatale précoce (mort à moins de 6 jours révolus). Cette définition est censée refléter l'ensemble des problèmes obstétricaux. La mortinatalité et la mortalité néonatale précoce sont donc liés.
Les données complètes ne semblent pas disponibles. En France, nous ne disposons pas des mortinatalités mensuelles et en Écosse, les mortalités néonatales précoces ne sont pas accessibles.
L'étude de la mortalité périnatale est indispensable et serait un bon indicateur.
En France, durant la campagne de vaccination, dès le 6 avril 2021, les femmes enceintes à partir du second trimestre étaient prioritaires. A cette période là, seules les personnes de plus de 70 ans pouvaient se faire vacciner. Le 12 avril, les personnes de plus de 55 ans ont pu se faire vacciner (Astrazénéca) et le 16 avril, les personnes de plus de 60 ans avec Pfizer et Moderna. C’est uniquement en mai que les personnes de 18 à 55 ans ont pu commencer à se faire vacciner. Beaucoup de personnes attendaient avec impatience le feu vert pour se faire injecter la « potion magique ». Y-a-t-il eu un afflux massif de femmes ayant déjà entamé leur second trimestre de grossesse, pressées, qui se sont faites vacciner dès cette période ?
Et si c’est le cas, y-a-t-il un lien avec le nombre excessif de bébés nés au mois de juin 2021 et décédés moins d'une semaine après leur naissance ? C'est une interrogation légitime. Nous manquons cruellement de données pour le savoir.
En Israël, nous pouvons constater une configuration proche. En effet, les deux pics de mortalité néonatale font suite à une campagne vaccinale pour femmes enceintes. Il y a eu une recommandation vaccinale en février 2021 aux futures mamans à partir de leur second trimestre de grossesse, donc deux mois avant le premier pic. Il y a eu une campagne pour le rappel des vaccinations, ciblant de manière agressive les femmes enceintes en août et septembre 2021, soit un à deux mois avant le deuxième pic.
Cette concommitance entre campagnes vaccinales pour les femmes enceintes, suivies de pics de mortalité néonatale dans ces deux pays est troublante et interroge.
Nous constatons que les trois pays étudiés ont des pics de mortalité néonatale à partir de 2021. Comment cela se fait-il ? D’où viennent ces excès de bébés morts à moins de 28 jours de leur naissance dans ces différents pays ? La cause est-elle la même ? Et qu’ont-ils en commun ? Les pics de mortalité apparaissent-ils systématiquement après une campagne de vaccination dédiée aux femmes enceintes ? Y-a-t-il d'autres pays dans le même cas ?
Une causalité vient à l’esprit : les vaccinations anti-covid19 effectuées en masse dans ces pays. Les femmes enceintes n’ont pas été exemptées de cette vaccination. Chaque pays a eu sa propre campagne de vaccination avec des choix différents de vaccins. Si cette hypothèse de causalité est facile et ne peut pas être validée à l’heure actuelle, elle ne peut en aucun cas être exclue. Il serait nécessaire pour pouvoir rejeter cette hypothèse de connaître le statut vaccinal des femmes ayant accouché, ainsi que la raison de la mortalité des nourrissons décédés prématurément.
Le docteur John Campbell en Écosse, a reçu une fin de non recevoir quand il a demandé le statut vaccinal des femmes écossaises enceintes ayant accouché. En Israël, l'assureur maladie a déclaré ne pas connaître le statut vaccinal des femmes enceintes. En France, le chercheur épidémiologiste Laurent Toubiana a essuyé le même type de déclaration quand il a demandé à connaître le statut vaccinal des personnes décédées.
Suite à ces excès de mortalité néonatale, une analyse approfondie devrait être effectuée. C'est quand même un comble que dans ces trois pays "civilisés", cela n'est soulevé aucune inquiétude, aucune recherche de causalité. Et d'autant plus, que nous sommes dans une situation sanitaire critique avec l'imposition de l'injection en masse de produits, dont les essais cliniques réglementaires ne sont toujours pas terminés.
Dans un État se souciant de sa population, des chercheurs habilités à manipuler des données médicales sensibles devraient avoir l’obligation de faire des analyses statistiques et biologiques afin d’évaluer avec précision le bénéfice/risque de ces injections imposées en masse. Dans l'état actuel des choses, tout semble devoir être dissimulé et ne fait que nourrir de sombres théories.
Vifs et chaleureux remerciements à Christel pour son aide à la vulgarisation et à la mise en forme de cet article.6) Annexes
A - Taux de mortalité infantile (0 à 1 an)
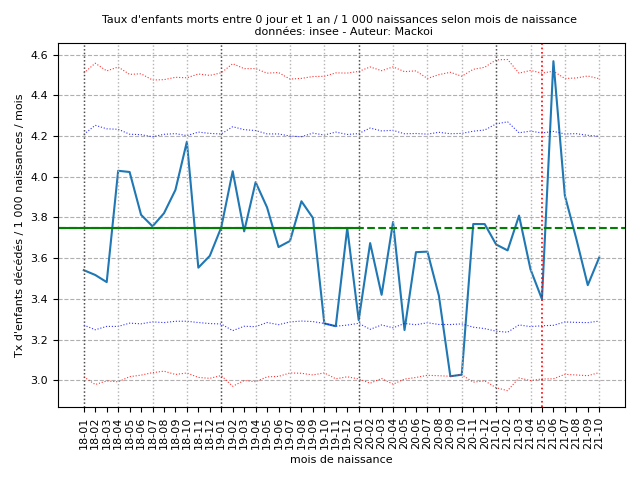
Taux de référence (janvier 2018-décembre 2019) = 3,75 décès / 1 000 naissances
lien : http://caillou5310.free.fr/index_alertez_bb.php#mort_inf_0_366
En 2020, tous les taux de mortalité infantile (de la naissance à un an) sont inférieurs à 3,8 / 1000, avec un taux de référence (2018 et 2019) égal à 3,75 / 1 000. Ceci indique une sous mortalité infantile des bébés nés en 2020 et explique pourquoi l’année 2020 a été exclue du taux de référence.
B - Taux de mortalité post néonatale (1 mois à 1 an)}
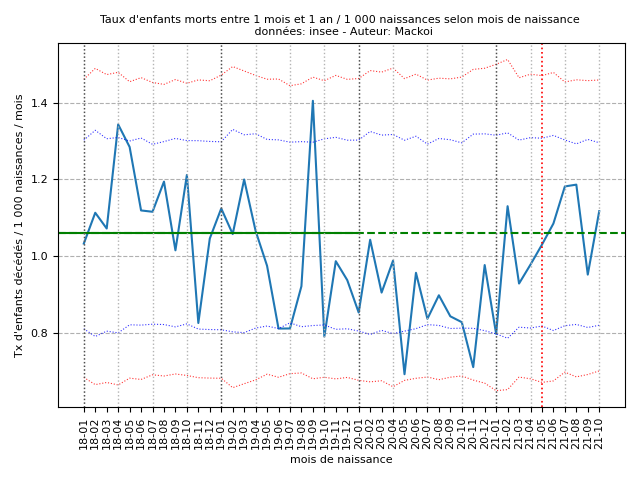
Taux de référence (janvier 2018-décembre 2019) = 1,06 décès / 1 000 naissances
lien : http://caillou5310.free.fr/index_alertez_bb.php#mort_inf_29_366
En 2020, aucun taux de mortalité post néonatale (entre 1 mois et un an) n’est supérieur au taux de référence (2018 et 2019). Ceci indique une sous mortalité post néonatale des bébés nés en 2020 et explique pourquoi l’année 2020 a été exclue du taux de référence.
C - Mortalité néonatale précoce (0 à 6 jours révolus)
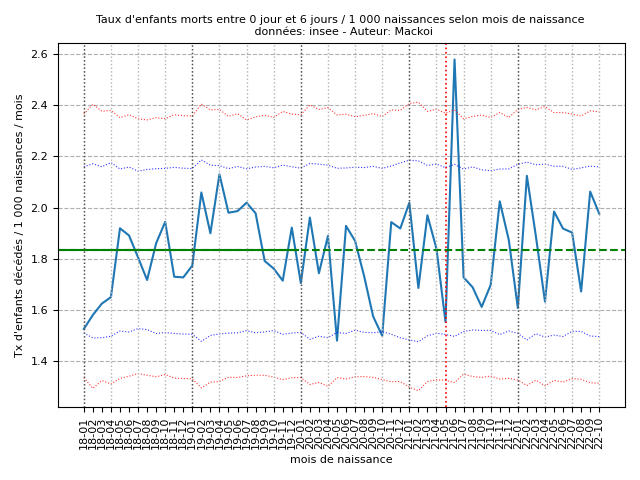
Taux de référence (janvier 2018-décembre 2019) = 1,83 décès / 1 000 naissances
lien : http://caillou5310.free.fr/index_alertez_bb.php#mort_inf_0_7
D - Mortalité néonatale tardive (7 à 28 jours révolus)
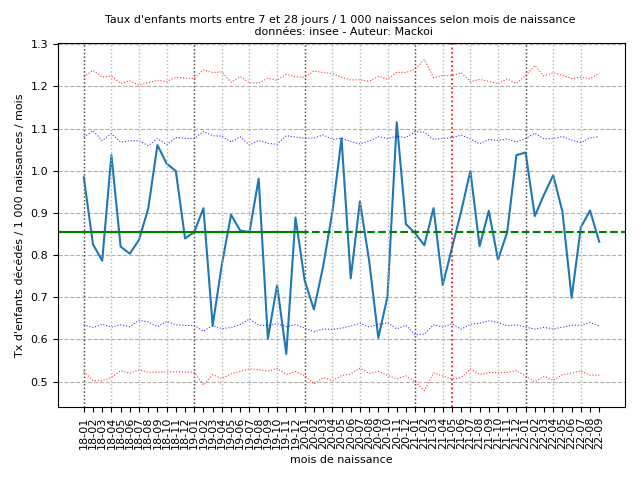
Taux de référence (janvier 2018-décembre 2019) = 0,85 décès / 1 000 naissances
lien : http://caillou5310.free.fr/index_alertez_bb.php#mort_inf_7_29
E - Mortalité à moins de 48h de vie
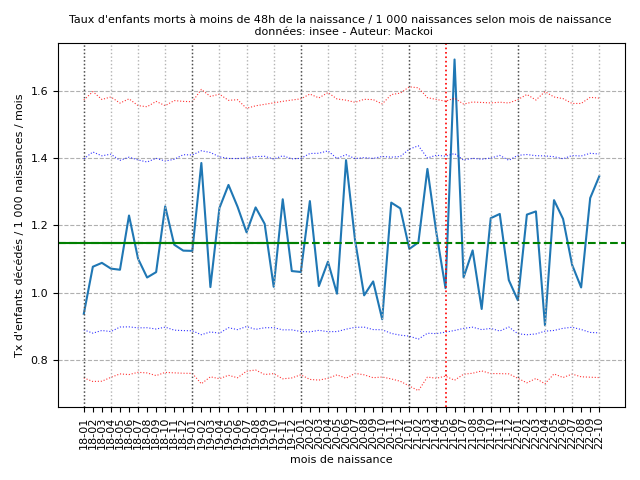
Taux de référence (janvier 2018-décembre 2019) = 1,15 décès / 1 000 naissances
lien : http://caillou5310.free.fr/index_alertez_bb.php#mort_inf_0_2
F - Mortalité entre 2 et 6 jours révolus de vie
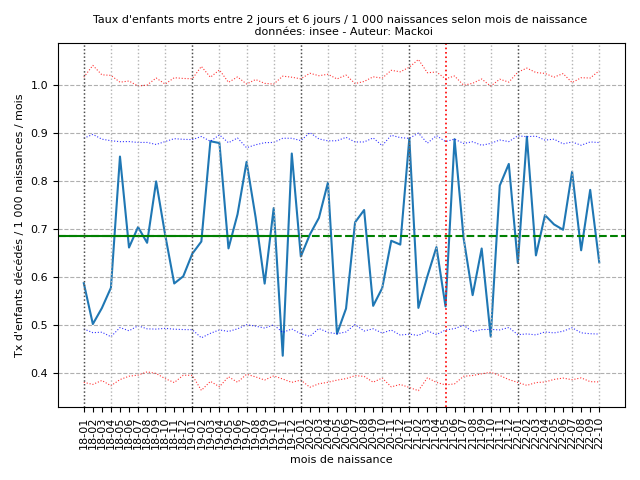
Taux de référence (janvier 2018-décembre 2019) = 0,69 décès / 1 000 naissances
lien : http://caillou5310.free.fr/index_alertez_bb.php#mort_inf_2_7
G - Mortalité néonatale écossaise avec loi de Poisson
Taux de référence (janvier 2018-décembre 2019) = 2,14 décès / 1 000 naissances
H - Loi de Poisson
La loi de Poisson est utilisée en statistique pour étudier la survenue des événements rares.
Pour cette analyse des différents taux de mortalité (néonatale, néonatale précoce, tardive, post néonatale, infantile, etc...), les taux de mortalité de référence ont été choisis de janvier 2018 à décembre 2019. Ils ont été calculés par le ratio du nombre de bébés décédés nés entre le 1er janvier 2018 et le 31 décembre 2019 sur le nombre de naissances de cette période.
Pour chaque type de mortalité, nous obtenons donc un taux de référence.
Soit t ce taux de mortalité de référence.
Soit n, le nombre de naissances pour un mois donné.
Le nombre de décès attendus pour ce mois est m = n × t
Le nombre de décès suit donc une loi de Poisson de paramètre m.
La probabilité que le nombre d’événements (décès) soit égal à k est : \(P(X=k) = \displaystyle e^{-m} \, \frac{m^k}{k!} \)
Calcul des bornes de intervalle de confiance \([m_1\,;\,m_2]\) à \(\textcolor{blue}{95 \%}\) (à \(\textcolor{red}{99,8 \%}\) ) :
- \(m_1\) : borne inférieure à \(\textcolor{blue}{95 \%}\) (à \(\textcolor{red}{99,8 \%}\) ):
recherche de \(m_1\) tel que \(P(k \leq m_{1}) = \displaystyle \sum\limits_{k=0}^{k = m_1} \frac{e^{-m} m^k}{k!} \geq \textcolor{blue}{0,025} \, \textcolor{red}{(0,001)} \) - \(m_2\) : borne supérieure à \(\textcolor{blue}{95 \%}\) (à \(\textcolor{red}{99,8 \%}\) ):
recherche de \(m_2\) tel que \(1-P(k \leq m_{2}) = \displaystyle 1 - \sum\limits_{k=0}^{k = m_2} \frac{e^{-m} m^k}{k!} < \textcolor{blue}{0,025} \, \textcolor{red}{(0,001)} \)
Exemple d'application pour le pic de mortalité néonatale du mois de juin 2021:
Du premier janvier 2018 au 31 décembre 2019, il y a eu 1 511 973 naissances vivantes.
Sur ces naissances, il y a eu 4 063 bébés décédés à moins de 28 jours révolus.
Le taux de référence est \(\displaystyle t = \frac{4\,063}{1\,511\,973} \simeq 0,00269\)
Ce qui donne un taux de référence de 2,69 décès pour 1 000 naissances.
Au mois de juin 2021, il y a eu \(n = 60 857\) naissances vivantes.
En faisant l'hypothèse que le taux de mortalité néonatale est le même que le taux de référence, le nombre de bébés décédés attendus parmi les bébés natifs du mois de juin est \(\displaystyle m = n \times t = 60\,857 \times \frac{4\,063}{1\,511\,973} \simeq 163,54\) bébés décédés.
Le nombre de bébés décédés suit la loi de Poisson de paramètre 163,54.
\[P(X=k) = e^{-163,54} \, \frac{163,54^k}{k!} \]- Calcul des bornes de intervalle de confiance \([m_{1}\,;\,m_{2}]\) à \(\textcolor{blue}{95 \%}\):
- \(m_1\): borne inférieure à \(\textcolor{blue}{95 \%}\)
recherche de \(m_1\) tel que \(P(k \leq m_{1}) = \displaystyle \sum\limits_{k=0}^{k = m_1} \frac{e^{-163,54} 163,54^k}{k!} \geq \textcolor{blue}{0,025}\)
\(\textcolor{blue}{m_1 = 139}\) - \(m_2\): borne supérieure à \(\textcolor{blue}{95 \% }\)
recherche de \(m_2\) tel que \(1-P(k \leq m_{2}) = \displaystyle 1 - \sum\limits_{k=0}^{k = m_2} \frac{e^{-163,54} 163,54^k}{k!} < \textcolor{blue}{0,025}\)
\(\textcolor{blue}{m_2 = 188}\)
Le nombre de bébés décédés a une probabilité de \(\textcolor{blue}{95 \%}\) d'être compris dans l'intervalle \(\textcolor{blue}{[139\, ; \, 188]}\).
Le nombre de bébés décédés a donc une probabilité de \(\textcolor{blue}{5 \%}\) de ne pas être dans cet intervalle (\(\textcolor{blue}{2,5 \%}\) d'être strictement inférieur à \(\textcolor{blue}{139}\) et \(\textcolor{blue}{2,5 \%}\) d'être strictement supérieur à \(\textcolor{blue}{188})\).
L'intervalle de confiance à \(\textcolor{blue}{95 \%}\) en taux de mortalité ( pour 1 000 naissances vivantes) est \(\textcolor{blue}{[2,28\,;\,3,09]}\). - \(m_1\): borne inférieure à \(\textcolor{blue}{95 \%}\)
- Calcul des bornes de intervalle de confiance \([m_{1}\,;\,m_{2}]\) à \(\textcolor{red}{99,8 \% }\):
- \(m_1\): borne inférieure à \(\textcolor{red}{99,8 \%}\)
recherche de \(m_1\) tel que \(P(k \leq m_{1}) = \displaystyle \sum\limits_{k=0}^{k = m_1} \frac{e^{-163,54} 163,54^k}{k!} \geq \textcolor{red}{0,001}\)
\(\textcolor{red}{m_1 = 125}\) - \(m_2\): borne supérieure à \(\textcolor{red}{99,8 \% }\)
recherche de \(m_2\) tel que \(1-P(k \leq m_{2}) = \displaystyle 1- \sum\limits_{k=0}^{k = m_2} \frac{e^{-163,54} 163,54^k}{k!} < \textcolor{red}{0,001}\)
\(\textcolor{red}{m_2 = 203}\)
Le nombre de bébés décédés a une probabilité de \(\textcolor{red}{99,8 \%}\) d'être compris dans l'intervalle \(\textcolor{red}{[125 ; 203]}\).
Le nombre de bébés décédés a donc une probabilité de \(\textcolor{red}{2 ‰}\) de ne pas être dans cet intervalle (\(\textcolor{red}{1 ‰}\) d'être strictement inférieur à \(\textcolor{red}{125}\) et \(\textcolor{red}{1 ‰}\) d'être strictement supérieur à \(\textcolor{red}{203})\).
L'intervalle de confiance à \(\textcolor{red}{99,8 \%}\) en taux de mortalité ( pour 1 000 naissances vivantes) est \(\textcolor{red}{[2,05\,;\,3,34]}\). - \(m_1\): borne inférieure à \(\textcolor{red}{99,8 \%}\)
Il y a eu 212 bébés décédés à moins de 28 jours parmi les 60 857 naissances vivantes du mois de juin 2021. Ceci donne un taux de 3,48 décès pour 1 000 naissances.
Ce nombre de naissances est en dehors de l'intervalle à 99,8 % et a donc une probabilité de moins de 2 ‰ de se produire.
Calcul de la probabilité qu'au moins 212 décès soient observés parmi les bébés natifs du mois de juin 2021: \[ \displaystyle 1 - P(X<212) = 1 - \sum\limits_{k=0}^{k = 211} \frac{e^{-163,54} 163,54^k}{k!} \simeq 0,00016 \]
La probabilité pour qu'il y ai au moins 212 bébés décédés est de 0,16 ‰ .
La programmation des calculs et des graphiques a été réalisée en python.
7) Sources
- nombre de naissances mensuels (site de l'insee): https://www.insee.fr/fr/statistiques/6523051?sommaire=5348638
- nombre de décès (site de l'insee): https://www.insee.fr/fr/statistiques/4487988?sommaire=4487854
- données écossaises (site de "Public Heatth Scotland"): https://scotland.shinyapps.io/phs-covid-wider-impact/
Pour la mortalité néonatale: cliquer sur l'onglet "Births and babies", puis "Stillbirths and infant deaths", puis sur "Neonatal deaths" - données israéliennes: Data on Neonatal Deaths from Major Israeli Health Insurer Shows Huge Spikes